前回は、龍安寺の石庭を計測してみるまでの経緯を書きました。
まず、細野氏が石庭の石の配置の基準になったと主張している、底辺:高さ:斜辺が1:2:√5の直角三角形から試してみます。私の自宅には、底辺:高さ:斜辺が1:2:√5の直角三角形の定規はないので、紙で同様の直角三角形をつくり、色々なパターンで、実測図に当ててみました。やはり、おさまりは良いとは思うものの、石庭の石の配置を十分に説明しているとは思えません。
石庭の縦、横の長さに綺麗にはまる直角三角形は、1:2:√5の直角三角形であり、これに関しては細野氏の発見は正しいと思います。しかし、石の配置の構図には、いくつもの直角三角形が使われており、この直角三角形が構図に使われていないとは言い切れないものの、よりはっきりとした基準があると感じます。
・石庭に綺麗におさまる直角三角形は 底辺:高さ:斜辺=1:2:√5の直角三角形のみなので、この直角三角形が龍安寺の石 庭の縦横の寸法の基準になっている。
・石の配置の構図としてはどちらとも言えない。(表現としては弱い)
さて、石庭の石の配置の基準に話を戻しますが、次に、小学生が使う内角が60度と30度の三角定規を石庭の実測図に当ててみました。すると、辺が石の側面と石と石の間を通るように見えました。これは何かあるかもしれない、と、思い、色々なパターンを当ててみます。その結果、私なりに石庭の石の配置の基準をいくつか見つける事ができました。(注1)
(写真1:図版引用『日本の庭園美 龍安寺』より野村勘治 実測図)
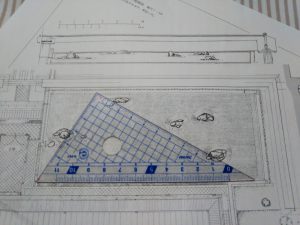

まず始めに、実測図の信憑性を調べるため、Google Earthを使って、石庭の上からの写真を探してみました。手元の定規で石庭の長辺、短辺と石の位置関係を測ってみましたが、実測図が正確だという判断をしました。石庭の長方形がわずかに歪んでいるという事も、ご理解頂けると思います。
(写真引用:Google Earth)

さて、準備が整ったので、具体的な説明に入りたいのですが、その前に、わかりやすく石の番号と、直角三角形の種類を書いておきたいと思います。

■ 直角三角形 A(底辺:高さ:斜辺=1:√3:2)、直角三角形B(同=1:1:√2)
その後、基準を変えて色々試してみましたが、現時点でもっとも適切と思われる三角形を作る規則は
1、直角三角形の90度ではない角の頂点が四隅a、b、c、fのいずれかに一致する。
2、90度の角度の頂点が、石庭の壁面に一致する。
3、斜辺が逆側の壁面に一致する。
4、直角三角形が,石と石の間、もしくは石の側面のラインを通る。(例外 直角三角形F)
というものです。
細野氏と一致しているのは
・直角三角形を使う事
・壁面に90度の頂点と斜辺を置く置き方
です。
・石のどこを基準とするか(側面、もしくは石と石の間)
においては全く考え方が違います。
次に、同様に直角二等辺三角形Bを基準点fに頂点を置いて描いてみました。実測図だと若干ずれるのですが、Google Earthの写真だと綺麗におさまります。今度は四つの石(5、6、8,14)の側面と一致しました。
これだけでも、大方の構図は決まってしまうと思うのですが、8~10の石群に当たるラインが一本だけなので、少し根拠が弱いような感じがします。
石の配置の最も強い基準になっているのは、正三角形を半分にした直角三角形Aだと思いますが、正方形を半分にした直角三角形Bも、小さい石の配置に関係していそうです。
こうなると、他の比率の直角三角形も関係していないか?という発想が浮かんできます。
ちょうど、昨年の秋にピタゴラス学派の世界観が詳しく書いてある、プラトンの『ティマイオス』という本を読んでおり、幾何学的、または幾何学を超えて、2、3、5の平方根とΦ(ファイ・黄金比)とπ(パイ・円周率)が非常に重要な数であるという思想があった事を知りました。
また、詳しい経緯は回を改めて書きますが、龍安寺の石庭の石の数が5、2、3、2、3と分かれていることで、恣意的ですが、5、2、3、2、3の数が2,3、5の平方根と、4の平方根=2、そして、Φ、πの整数の近似値を表しているのではと考え、試してみることにしました。
■ 直角三角形C(底辺:高さ:斜辺=1:√2:√3)

直角三角形C(注3)は、底辺:高さ:斜辺≒1:1.41:1.73 になり、三角形の頂点の内角が35.6度と54.4度になります。手元の分度器では、0.1度の計測はできないので、35度と55度とします。四隅の角に頂点をあわせて直角三角形Cを置いてみると、上向きの三角形は8、9番の石の間と、13、15番の石の間、6番の側面を通ります。Cに頂点を取った同じ三角形は、5番の側面と11番の側面を通ります。
■ 直角三角形D(底辺:高さ:斜辺≒1:1.272:Φ1.618)
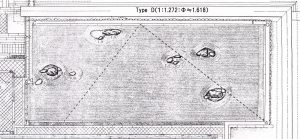
直角三角形Dの比率は、底辺:高さ:斜辺≒1:1.272:1.618 になります。
角度は、38.5度と51.5度になりますが、近似値をとって38度と52度にします。頂点aに内角38度を合わせた三角形が15番、9番の側面と通ります。二辺が石と接する三角形は見つけられませんでした。
■ 直角三角形E(底辺:高さ:斜辺≒1:2.98:3.14)

残るは、πです。斜辺がπ(3.14)の三角形の比率は、底辺:高さ:斜辺≒1:2.98:3.14です。角度は18.7度と61.3度になります。残っている石、2,3、7、10番です。2,3に線を引いてみると頂点fとした底辺:高さ≒1:3の直角三角形ができます。上の壁面の頂点から、18~19度で線を引くとちょうど、7、8、10番の側面を通ります。3番の石は、1番との間の関係がありますから位置が決まります。これで全ての石が直角三角形のラインと関係し、ほとんどの石の位置が決まりました。
2、7、10、に関しては、ライン上で多少石の位置を動かしても成り立つので、石庭の石の位置関係が完全に解けたわけではありません。強いて言えば、十五の石が五群に分けるには、ライン上で石群に近いところに置かなければいけない、という事もあると思いますが、これについては現段階での判断は避けたいと思います。
■ より厳しい条件での検証
石庭自体は鑑賞するものであり、また、日本の芸術の特徴として、全てを表現せずある部分を隠すという特徴があります。
しかし、検証というと厳密さが求められるので
・二辺に石のポイントが接しており、直角三角形を表現できる。
という基準を満たす、直角三角形を抜き出してみました。

この基準でも、おおよその石の位置の基準を説明することができます。
結論として、
龍安寺の石庭の石の配置は、
①底辺が1で、斜辺が√2、√3、2、πの直角三角形(ピタゴラスの定理)が基準として使われている
②石庭の縦横の長さの基準に底辺:高さ:斜辺が1:2:√5の直角三角形が使われている。(『五十五の推理』より)
と言えるのではないかと思います。(注4)
また、もう図版を測っていてもう一つ気がついた事ですが、左側の壁のcdとef(段差で中央に出ている部分と、出ていない部分)の比が3.7㎝:2.3㎝(160分の1)=1.61:1になっており、黄金比(Φ:1)がわかっていたのではないかと考えられます。
もちろんこれらの基準を使っても、色々な組み合わせの配置が考えられるので、最終的になぜこの位置になったのかが、わかったわけではありません。
更に奥の深い幾何学的な法則が法則が隠れているかもしれませんし、他の思想面も含めて配置を決めたのかもしれません。しかし、宗教や人種を超えて、龍安寺の石庭が世界中の人々を惹きつけているのは、15の石の配置と、なぜそれが魅力的なのか?とう事だと、私は考えています。
細野氏の『謎深き庭 龍安寺石庭 十五の石をめぐる五十五の推理』では、最後の推理五十五は読者への問いになっているため、五十四の説が取り上げられています。
他の枯山水で、このような事は起こりませんし、単純な美しさとは違う魅力を兼ね備えているからこそ、このような現象が起こるのでしょう。
そのような意味では、幾何学的な基準というのは重要なポイントだと考えています。
では、なぜ、2、3、5の平方根とπという数を意図的に選んだのか?という疑問が出てくると思います。これらの数は古代エジプトの数学から、プラトン、そして現代に至るまで、幾何学において非常に重要な数とされています。
次回はこの数について書きたいと思います。
注3:
細野透氏も著書で、大和白銀比として斜辺が√3の三角形を扱っていますが、√3の着想得た根拠と、三角形の当て方、解釈が全く違うので別物として考えています。
注4:誤差について
直角三角形のラインを引く時に、微妙なずれが生じるのですが
・そもそも石庭そのものの四隅が厳密な直角ではなく、微妙にゆがんでいる。
・石と石との間の空間や、凹凸がある側面のラインをつかっているので厳密な定義ができない。
・最小限の石で、対象を表現するために、誤差を承知で石庭をつくっていると思われる。仮に、誤差なくもっと正確に表現しようとすれば、より多くの石を使う事になるが、それでは意味がない。音楽で例えると、楽曲のメロディと情感を分けて鑑賞者に伝えるのは芸術的とは言い難く、音程を微妙にずらしたりビブラートをかけたりしながら、楽曲と情感を同時に伝える事のほうが芸術的と言える。同時にいくつかのものを表現する(多機能性)のが芸術の条件でもある。
以上の理由で、鑑賞者が対象を認識できる範囲内である限り、誤差は認められるもの、芸術の本質に必要なものと考えます。









この投稿へのコメント